Saturday, August 1, 2020

ABSTRACT ALGEBRA - 2018 | B.SC CS 2ND YEAR | MJPRU | EXAM PAPER | My CS Tutorial

My CS Tutorial August 01, 2020

Aabstract algebra | My CS Tutorial

Paper code: 13511
1511
B.Sc. (Computer Science) (Part 2)
Examination-2018
Paper No. 1.2
ABSTRACT ALGEBRA

Time: Three Hours][Maximum Marks: 50

Note: Attempt five questions in all selecting at least one question from each Section. All questions carry equal marks.

Section-A

1. (a) Show that the set of matrices:

$A_{\alpha} = \begin{bmatrix} \cos \alpha &-\sin \alpha \\\sin \alpha & \cos \alpha \end{bmatrix}$

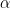Where $\alpha$ is a real number, forms a group under matrix multiplication?

(b) Prove that the set of all n nth roots of unity forms a finite abelian group of order n with respect to multiplication.

2. (a) Show that every permutation can be expressed as a product of disjoint cycles.

(b) Show that a necessary and sufficient condition for a non-empty subset H of a group G to be a subgroup is that :

$a,b \in H \Rightarrow ab^{-1} \in H$

where $b^{-1}$ is inverse of b in G.

3. (a) Show that order of each subgroup of a finite group is a divisor of the order of the group.

(b) Show that every group of prime order is cyclic.

Section-B

4. (a) Show that intersection of any two normal subgroup of a group is a normal subgroup.

(b) State and prove fundamental theorem on homomorphism of groups.

5. (a) Show that ever field is an integral domain.

(b) Show that a ring R is withput zero divisors if and only if the cancellation laws holds in R.

6. (a) Show that intersection of two subrings of a ring R is also a subring of R.

(b) Show that S is an ideal of S+T, where S is any ideal of ring R and T an subring of R.

Ssection-C

7. (a) If f is a homomorphism of a ring R into a ring R’ with kernel S, then S is an ideal or R.

(b) An ideal S of the ring of integers I is maximal iff S is generated by some prime integer.

8. (a) Show that union f two subspaces is a subspace if and only if one is contained in the other.

(b) Prove that if two vectors are linearly dependent, one of them is a scalar multiple of the other.

9. (a) Show that the three vectors (1, 1, -1), (2,-3, 5) and (-2, 1, 4) of R3 are linearly independent.

(b) if W be a subspace of a finite dimensional vector-space, then show that :

$\dim \frac{V}{W} = \dim V - \dim W$

10. Discuss the direct sum of subspaces and show that the necessary and sufficient conditions for a vector space V(F) to be a direct sum of its two subspaces W1 and W2 are that :

(i) $V = W_{1} + W_{2}$

(ii) $W_{1} \cap W_{2} = \left \{ \bar{O} \right \}$

_______________________________________

Please share this post and blog link with your friends.For more programs use this blog.

If you have any problem, please comment in comment box, subscribe this blog for notifications of new post on your email and follow this blog.If you have any method of this tutorial or program or want to give any suggestion send email on hc78326@gmail.com

Created by-- HARSH CHAUHAN

About My CS Tutorial
SoraTemplates is a blogger resources site is a provider of high quality blogger template with premium looking layout and robust design. The main mission of SoraTemplates is to provide the best quality blogger templates.