 |
| Numerical analysis | My CS Tutorial |
Paper code: 13512
1512
B.Sc. (Computer Science) (Part 2)
Examination, 2018
Paper No. 1.3
NUMERICAL ANALYSIS
Time: Three Hours]
[Maximum Marks: 50
Note: Attempt five questions. All questions carry equal marks. Symbols are as usual. Use of calculator is allowed.
1. (a) Evaluate :
(b) If :
find  .
.
2. (a) Given :
and  . Find
. Find  .
.
(b) Find y, when x = 8 for :
3. (a) If  , find the divided differences
, find the divided differences  ,
,  and
and  .
.
(b) Given lof 654 = 2.8156, log 658 = 2.8182, log 659 = 2.8189 and log 661 = 2.8202. Find log 656.
4. Solve the following system by iteration method :
5. Solve the system :
by :
(i) Gauss’s elemination method
(ii) Gauss’s Jordan method
6. (a) Evaluate :
by using Simpson’s 3/8 rule.
(b) If  , prove that:
, prove that:
and hence find :
7. (a) Evaluate :
by Weddle’s rule.
(b) Using Euler’s modification method to compute y for x = 0.05. Given that :
with the initial condition x0 = 0 and y0 = 1.
8. Solve initial value problem :
for x = 0.4, 0.5 by using Milne’s method when it is given :
9. Solve :
for x = 0.5 and x = 1.0 by using Runge-Kutta method, with x =0, y = 1, y’ = 0.
10. (a) Find 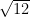 to five places of decimal by Newton’s-Raphson method.
to five places of decimal by Newton’s-Raphson method.
(b) Compute the real root of  correct to five decimal places by Regula-Falsi method.
correct to five decimal places by Regula-Falsi method.
_______________________________________
Please share this post and blog link with your friends.For more programs use this blog.
If you have any problem, please comment in comment box, subscribe this blog for notifications of new post on your email and follow this blog.If you have any method of this tutorial or program or want to give any suggestion send email on hc78326@gmail.com
Created by-- HARSH CHAUHAN














No comments:
Post a Comment